System Identification 2016

Lecturer: Lucian Busoniu, TA: Zoltan Nagy

Navigation: [Schedule|Course material|Labs|Lab tests|Project|Contact]          [Back to Lucian Busoniu's webpage]

The course introduces nonparametric methods for system identification, as well as parametric methods including prediction error and instrumental variables techniques. It describes the material at an appropriate BSc level, and builds in a self-contained manner the required mathematical background. The course is based on the book by Soderstrom and Stoica.

This course is part of the Bachelor program of the Automation Department, UTCluj (3rd year 1st semester). Prerequisites: linear dynamical systems, linear algebra, statistics. The lecturer is Lucian Busoniu, while Zoltan Nagy helps with lab classes.

Grading:

• 40%=2x20% two lab test, each one-hour long, in which randomly chosen methods studied at previous labs must be applied. The solution consists of Matlab code, which must be submitted at the end of the test. The code will be run and verified by the lecturer; any non-original solutions are disqualified. See the schedule for the test slots.
• 20% project, see its section below for details.
• 30% final exam.
• (new this year) 20% lab questions: a short (5 minutes) written assignment at the start of each lab, consisting of a couple of questions from the lecture material relevant to that day's lab. For the first lab, by exception, this is done at the end.

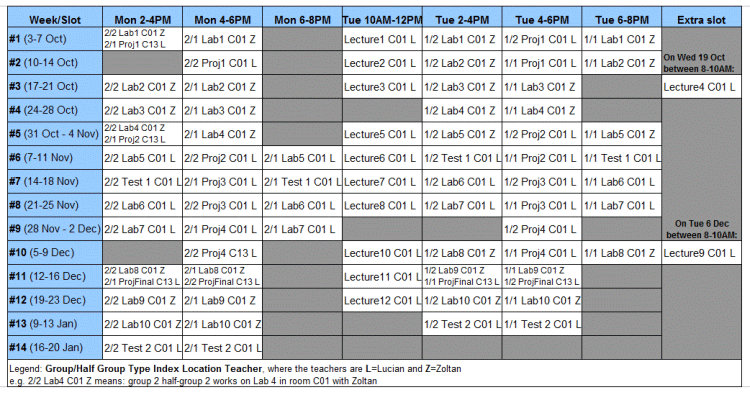
Dates and locations:

• Lectures: Tuesdays 10AM-12PM in C01 (Dorobantilor street). There are 12 lectures in total.
• Labs & project: group 1 Tuesday afternoons; group 2 Monday afternoons, in C01 and C13 (Dorobantilor street). We will have 10 labs and 5 project sessions for each half-group.

Due to dependencies between lectures, labs, and project material, as well as other constraints, the schedule of the labs and project sessions is rather complicated. Please look at it carefully to determine exactly when you have to be in the classes:

Update 29 Nov: Emergency reschedule due to no attendance at lecture 9.

Course material

The lecture slides are mandatory reading; they will be written down in detail to give a self-contained, complete picture of the topics. They are made available here in time for each lecture.

• Part 1: Introduction to System Identification (covered in lecture 1; PDF).
• Part 2: Transient Analysis of Step and Impulse Responses (covered in lectures 2 and 3; PDF).
• Part 3: Mathematical Background: Linear Regression and Statistics (covered in lectures 4 and 5; PDF).
• Part 4: Correlation Analysis (covered in lecture 5; PDF).
• Part 5: Prediction error methods (covered in lectures 6, 7, 8; PDF, updated 14 Nov).
• Part 6: Instrumental variable methods (covered in lecture 9; PDF).
• Part 7: Input signals (covered in lecture 10; PDF, updated 12 Dec with some typo corrections).
• Part 8: Recursive identification methods (covered in lecture 11; PDF).
• Part 9: Model validation and structure selection (covered in lecture 12; PDF).

In addition to the slides, followers may optionally consult the following books:

• T. Soderstrom and P. Stoica. System Identification. Prentice Hall, 1989. The full text of this book is available at: http://user.it.uu.se/~ts/bookinfo.html. This book forms the basis of the course.
• L. Ljung, System Identification: Theory for the User, 2nd ed., Prentice Hall, 1999.

• Lab 1: Matlab exercises (PDF) -- two short exercises in order to get re-acquainted with Matlab. For a brief intro to Matlab, have a look at the following document (with thanks to Paula Raica for allowing us to use it): http://rocon.utcluj.ro/st/Files/ST_Lab1.pdf.
• Lab 2: Transient Analysis of Step Responses (PDF). The data files are: for first-order systems, #1, #2, #3, #4, #5, #6, #7, #8 (where # stands for index). For second-order systems, #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 3: Transient Analysis of Impulse Responses (PDF). The data files are: for first-order systems, #1, #2, #3, #4, #5, #6, #7, #8. For second-order systems, #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 4: Linear Regression for Function Approximation (PDF). Download the rbfapprox function, as well as the lab4_template script. The data files are: #1, #2, #3, #4, #5, #6, #7, #8, #9, #10, #11, #12, #13, #14, #15.
• Lab 5: Correlation analysis (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 6: ARX model identification (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 7: Prediction error methods (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 8: Instrumental variable methods (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8.
• Lab 9: Pseudo-random binary sequences (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8. Download the system simulator as well: simulateid.p.
• Lab 10: Recursive identification. Model validation using correlation tests (PDF). The data files are: #1, #2, #3, #4, #5, #6, #7, #8.

The first lab test will take place on 8 November 2015 (group 1) and 14 November 2015 (group 2), in the lab slots (2-4 and 6-8PM). Each student is assigned a randomly chosen technique studied in labs 2-5, and a randomly chosen dataset; the student must then apply the technique to the dataset. The solution must be developed in the first 50 minutes; the last 10 minutes are reserved for discussing the solution with the lecturer. Please be on time; the one-hour interval cannot be exceeded since your colleagues are starting the test immediately after that.

The solution consists of Matlab code, which must be submitted at the end of the test, and will be run and verified by the lecturer. To ensure the test is solvable in the time slot allowed, some techniques can be applied in a simplified manner, e.g. for step response analysis, values can be read directly on the graph rather than programatically computed. These simplifications will be explicitly indicated in the test material.

You are free to use the course material, including lecture slides, lab descriptions and data, and the startup example code which was made available for some labs. All this will be available offline on the computer on which you will take the test. The complete Matlab documentation is of course also available. However, the internet connection is disabled on the computer and you are not allowed to use internet-connected devices, or to reuse the solutions you developed for the labs.

For the first test, the slots are assigned as follows: Lab test 1 schedule (PDF), where the format is: date (8 or 14, both in November 2015) / hour. If for well-founded reasons you cannot make it on the assigned slot, please contact the lecturer as soon as possible with a request to change the slot. Reassignments cannot be made if they result in more than 8 students taking the test in the same time slot. Note that before test 1, everyone should have labs 2-5 submitted; if not please correct this ASAP.

Project: Black-box modeling using neural networks

The project aims to move beyond the linear-system case treated in the lectures. Nonlinearities characterize virtually every real system, and in certain circumstances they cannot be sufficienty approximated by linear dynamics, making nonlinear models necessary. This project deals with a neural-network based method for the black-box identification of nonlinear systems.

The assignment is Matlab-based and consists of two problems, both using feedforward neural networks. In the first problem the neural network is used to model the behavior of an unknown nonlinear but static function, where the outputs are affected by noise. This problem is a stepping stone to the dynamical modeling case, and also serves to familiarize the students with neural networks. The second problem concerns data-driven black-box modeling of an unknown dynamical system.

The project will be performed in groups of two students, and every group gets their own data files. The deliverables include a PDF report and the Matlab code. More details, including the deadlines, can be found in the project description (PDF). Please read it carefully. In order to obtain the first two reference documents on neural networks, append the following to the course website address (busoniu.net/teaching/sysid2016): /projectfiles/nnref_Babuska.pdf, /projectfiles/nnref_Jainetal.pdf and then save the files on your computer.

Contact

Comments, suggestions, questions etc. related to this course or website are welcome; please contact either the lecturer or the TA at the addresses below (given as images for spambot protection).